When designing mechanical system that requires multiple parts to fit together within a confined space, tolerances will significantly influence the assembly’s functionality. To gain insight into the compatibility and performance of the assembled design, a Tolerance Chain Analysis should be performed. This analysis uses a pair of simple equations to determine the minimum and maximum space available for assembly, often referred to as S.
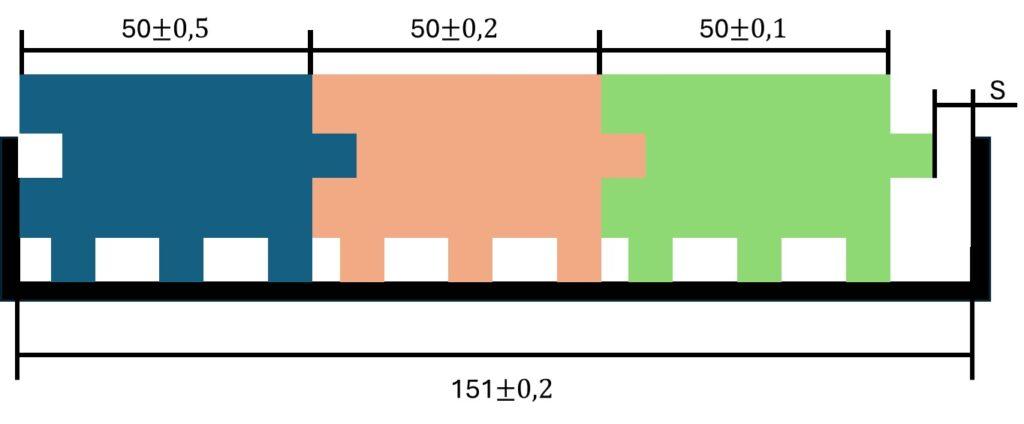
Illustration example, consider a container with three similar blocks inside, each having individual sizes that vary due to fabrication tolerances. The technology used for fabricating these parts affects the design’s function, assembly, and operational quality.
For example,
- The Blue block is manually manufactured on a milling machine.
- The Orange block is produced on an older CNC machine.
- The Green block is made using a state-of-the-art CNC machine.
The different manufacturing technologies and conditions impact the tolerances of the parts. Therefore, it is crucial to consider manufacturing processes when performing a Tolerance Chain Analysis.
What is Variation and Why is it Important?
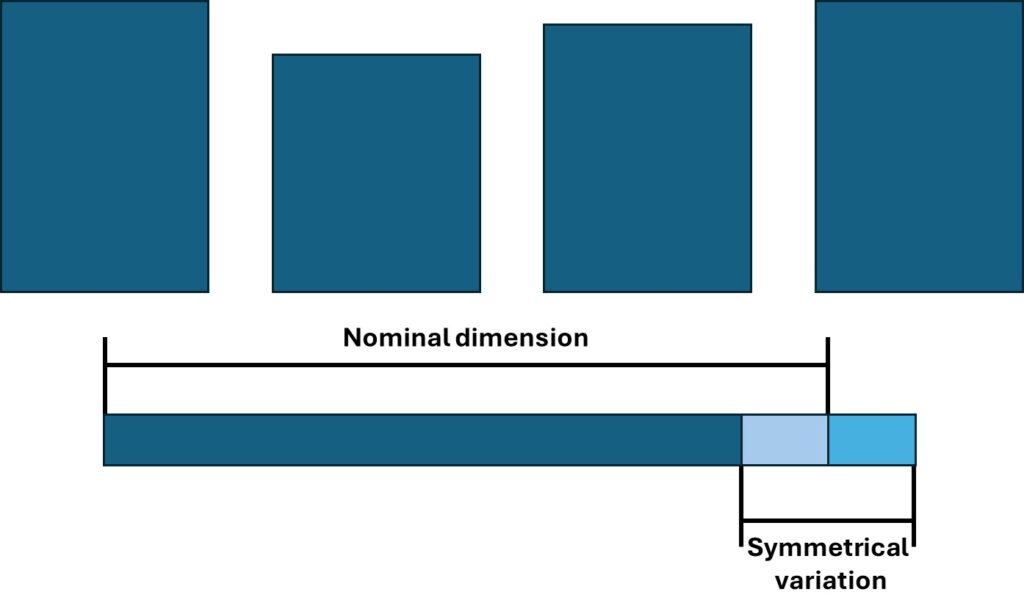
The illustration depicts four cylindrical parts, each cut to the same height but exhibiting different heights due to manufacturing tolerances. As a result, the parts you incorporate into your design will not match the exact dimensions required, being either marginally too small or too large.
Setting Up the Tolerance Chain Analysis.
To understand how a Tolerance Chain Analysis works it is best to consider the Worst-Case scenarios. This approach assumes that each part is either at its minimum or maximum size, with intermediate sizes disregarded. This results in two critical scenarios to evaluate.
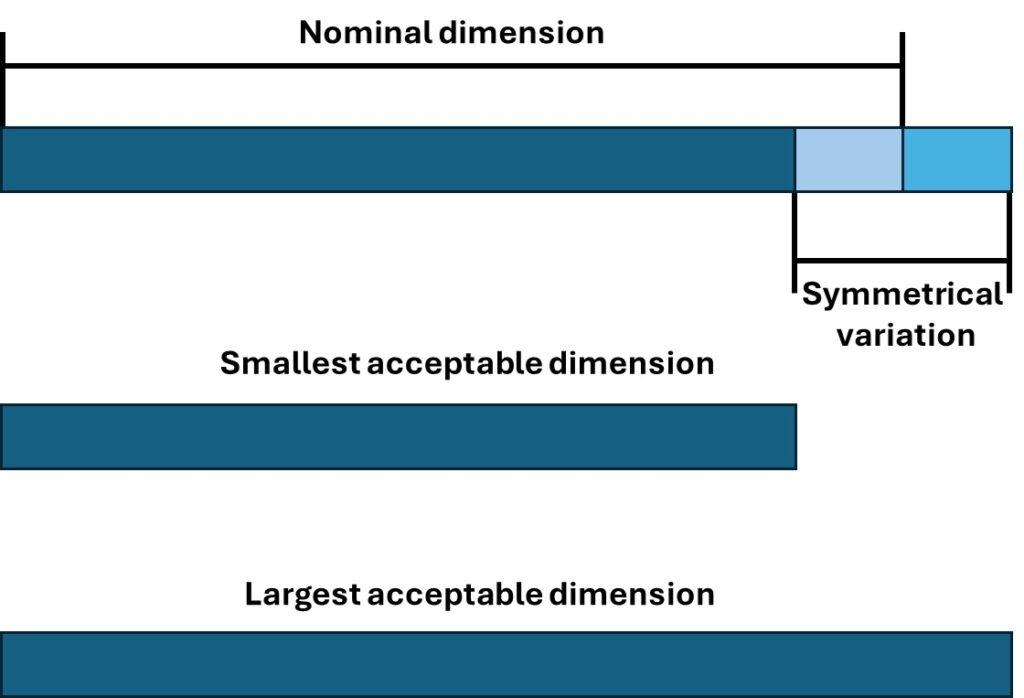
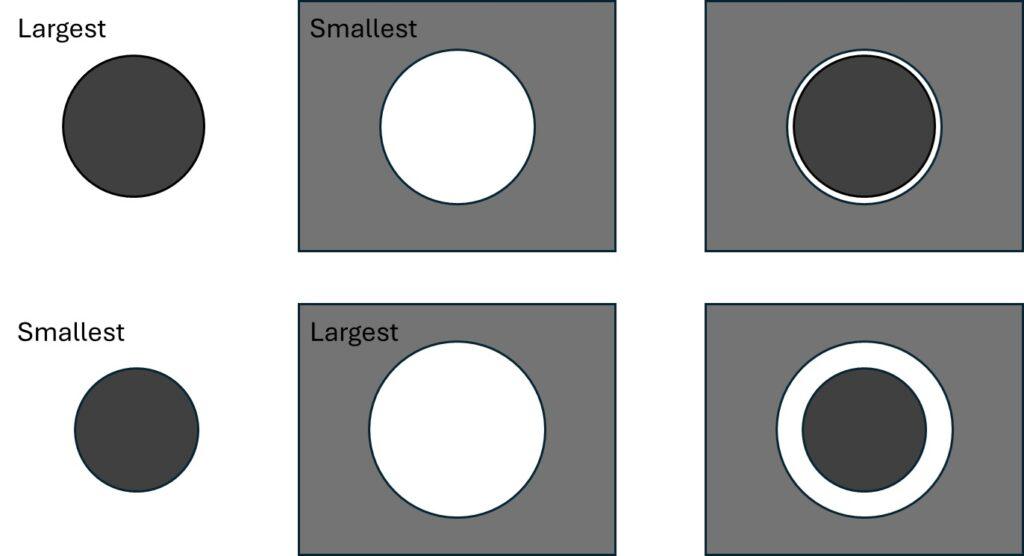
From the Worst-Case Analysis, two equations can be derived to describe the smallest and largest space for assembly. These equations calculate the space between connecting bodies. It is important to remember that negative space is possible in this context if you have a solution that requires a press-fit or similar. All loose fittings must have a positive space to be possible to assemble.
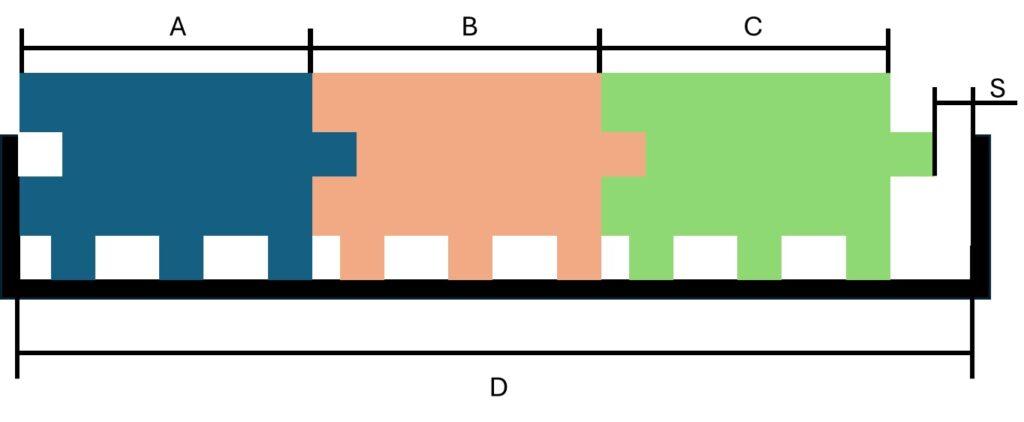
In the illustration, the sizes of A, B, C, and D determine the space S. Using the Worst-Case scenario, two equations can be derived.
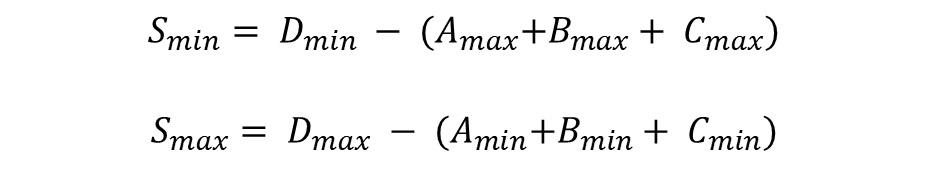
When tolerances are inserted into these equations, the assembly space range is derived. From this, it is possible to determine if the assembly is feasible for the entire tolerance chain.
Example Calculation from illustration:

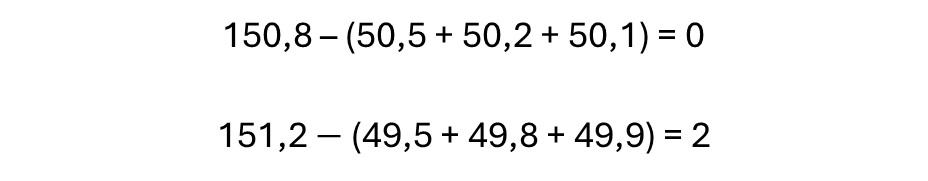
From the example, the space varies from 0 to 2 mm. In any application, S = 0 or S < 0 mm space is always problematic and must be further evaluated before it is accepted as a viable solution.
This analysis ensures that all parts will fit together within the specified tolerances, leading to a successful assembly and functional design.
Summery
Tolerance Chain Analysis is crucial for ensuring the compatibility and functionality of mechanical designs with multiple parts. This analysis uses equations to determine the maximum and minimum assembly space, factoring in manufacturing tolerances. Variation in part sizes due to fabrication processes must be managed to ensure proper assembly. By analyzing the worst-case scenarios, designers can predict if the parts will fit together correctly. This helps identify potential issues early, ensuring the design’s success.
Good luck with your project!




